Background
Backpropagation is a common method for training a neural network. There is no shortage of papers online that attempt to explain how backpropagation works, but few that include an example with actual numbers. This post is my attempt to explain how it works with a concrete example that folks can compare their own calculations to in order to ensure they understand backpropagation correctly.
Backpropagation in Python
You can play around with a Python script that I wrote that implements the backpropagation algorithm in this Github repo.
Continue learning with Emergent Mind
If you find this tutorial useful and want to continue learning about AI/ML, I encourage you to check out Emergent Mind, a new website I’m working on that uses GPT-4 to surface and explain cutting-edge AI/ML papers:

In time, I hope to use AI to explain complex AI/ML topics on Emergent Mind in a style similar to what you’ll find in the tutorial below.
Now, on with the backpropagation tutorial…
Overview
For this tutorial, we’re going to use a neural network with two inputs, two hidden neurons, two output neurons. Additionally, the hidden and output neurons will include a bias.
Here’s the basic structure:

In order to have some numbers to work with, here are the initial weights, the biases, and training inputs/outputs:
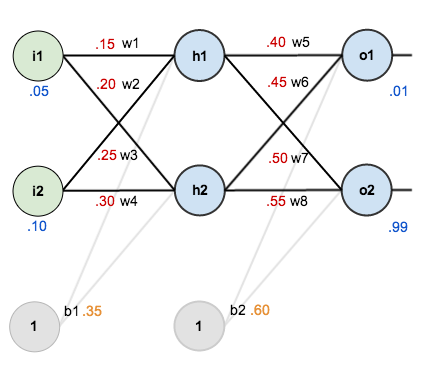
The goal of backpropagation is to optimize the weights so that the neural network can learn how to correctly map arbitrary inputs to outputs.
For the rest of this tutorial we’re going to work with a single training set: given inputs 0.05 and 0.10, we want the neural network to output 0.01 and 0.99.
The Forward Pass
To begin, lets see what the neural network currently predicts given the weights and biases above and inputs of 0.05 and 0.10. To do this we’ll feed those inputs forward though the network.
We figure out the total net input to each hidden layer neuron, squash the total net input using an activation function (here we use the logistic function), then repeat the process with the output layer neurons.
Here’s how we calculate the total net input for :
We then squash it using the logistic function to get the output of :
Carrying out the same process for we get:
We repeat this process for the output layer neurons, using the output from the hidden layer neurons as inputs.
Here’s the output for :
And carrying out the same process for we get:
Calculating the Total Error
We can now calculate the error for each output neuron using the squared error function and sum them to get the total error:
For example, the target output for is 0.01 but the neural network output 0.75136507, therefore its error is:
Repeating this process for (remembering that the target is 0.99) we get:
The total error for the neural network is the sum of these errors:
The Backwards Pass
Our goal with backpropagation is to update each of the weights in the network so that they cause the actual output to be closer the target output, thereby minimizing the error for each output neuron and the network as a whole.
Output Layer
Consider . We want to know how much a change in
affects the total error, aka
.
By applying the chain rule we know that:
Visually, here’s what we’re doing:

We need to figure out each piece in this equation.
First, how much does the total error change with respect to the output?
is sometimes expressed as
When we take the partial derivative of the total error with respect to , the quantity
becomes zero because
does not affect it which means we’re taking the derivative of a constant which is zero.
Next, how much does the output of change with respect to its total net input?
The partial derivative of the logistic function is the output multiplied by 1 minus the output:
Finally, how much does the total net input of change with respect to
?
Putting it all together:
You’ll often see this calculation combined in the form of the delta rule:
Alternatively, we have and
which can be written as
, aka
(the Greek letter delta) aka the node delta. We can use this to rewrite the calculation above:
Therefore:
Some sources extract the negative sign from so it would be written as:
To decrease the error, we then subtract this value from the current weight (optionally multiplied by some learning rate, eta, which we’ll set to 0.5):
We can repeat this process to get the new weights ,
, and
:
We perform the actual updates in the neural network after we have the new weights leading into the hidden layer neurons (ie, we use the original weights, not the updated weights, when we continue the backpropagation algorithm below).
Hidden Layer
Next, we’ll continue the backwards pass by calculating new values for ,
,
, and
.
Big picture, here’s what we need to figure out:
Visually:
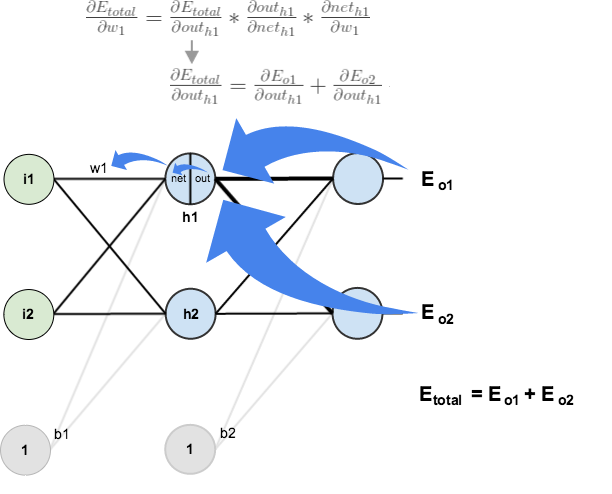
We’re going to use a similar process as we did for the output layer, but slightly different to account for the fact that the output of each hidden layer neuron contributes to the output (and therefore error) of multiple output neurons. We know that affects both
and
therefore the
needs to take into consideration its effect on the both output neurons:
Starting with :
We can calculate using values we calculated earlier:
And is equal to
:
Plugging them in:
Following the same process for , we get:
Therefore:
Now that we have , we need to figure out
and then
for each weight:
We calculate the partial derivative of the total net input to with respect to
the same as we did for the output neuron:
Putting it all together:
You might also see this written as:
We can now update :
Repeating this for ,
, and
Finally, we’ve updated all of our weights! When we fed forward the 0.05 and 0.1 inputs originally, the error on the network was 0.298371109. After this first round of backpropagation, the total error is now down to 0.291027924. It might not seem like much, but after repeating this process 10,000 times, for example, the error plummets to 0.0000351085. At this point, when we feed forward 0.05 and 0.1, the two outputs neurons generate 0.015912196 (vs 0.01 target) and 0.984065734 (vs 0.99 target).
If you’ve made it this far and found any errors in any of the above or can think of any ways to make it clearer for future readers, don’t hesitate to drop me a note. Thanks!
And while I have you…
Again, if you liked this tutorial, please check out Emergent Mind, a site I’m building with an end goal of explaining AI/ML concepts in a similar style as this post. Feedback very much welcome!

nice explanation.
Hey Matt. I’m stuck here: I got dEo2/douth1=-0.017144288. you got -0.019049. Can you check again?
Dude….die
@H.Taner Unal
You got that result because you identified dnet02 / douth1 as weight w6 (0.45), when it is actually w7 (0.5). The way they are labeled on the graph is somewhat counterintuitive.
Nicely explained. Thanks :)
Very helpful. Thanks
Thank you a lot! Didn’t get on lecture.Here is the best explanation!
To get the net input of h1 you need to calculate w1*i1 + w3*i2 + b1*1. The weight w2 does not connect to h1
It can look like that in the pictures, however h1 is in fact from w1 and w2. The weight # is created based off of the hidden layer. For example h1 has w1 and w2 while h2 has w3 and w4.
If we want to extend this to a batch of training samples, do we calculate the output layer errors simply by averaging the error at each output over the training samples, then obtain the total by summing the averages?
e.g. E[O][1] = sum between 1 and N of E[O][1][n], where n is the training sample index and {1 <= n <= N} (Is that correct?)
EDIT – forgot to divide sum by N
I want to thank you for this write up. Best one on the net! Your breakdown of the math is incredibly helpful
Don’t we need to update b1 and b2?
For really basic NN’s, it is not needed and can be left alone. Think of the biases as shifting your graph while the weights change the slope. If you wish to update the biases, simply do the same thing as the weights but don’t add the previous node as it is not attached to it. For example b2 is the same as w5, but without the hiddens (w5 would be h1) because it is not connected to any hiddens. b1 is the same as w1 but without the hidden stuff like h1(1-h1). Hope this helps, if not just leave another question.
Sorry but I messed this up, the h1(1-h1) would be removed for b2 NOT b1, as b1 connects to hidden layer and the b2 does not. For b1 you would remove the input (i1) stuff.
This is really amazing.thankyou for the clear explanation.
Excuse me. If I have 1000 training data, In bckpropagation, the loss function would be E=sum((target1-out1)^2+(target2-out2)^2+……(target1000-out1000)^2), should partial derivative of the weights to E be divided by 1000(the number of data) when update the weights
Wonderful explaination!, btw how to reduce biases at input and hidden layer?
Bravo Matt, la migliore spiegazione!
Hey Matt, I’ve been trying to duplicate your results in a network I am building, and running into an issue. Using your examples as my test data, I have passed all tests except for the weight values in w6 and w7. My values are not matching.
From a sniff test perspective, w6 appears it should be increasing since the output is lower than the expected (0.7 -> ~0.9) , but your calculation has the weight being reduced (0.45 -> ~0.41). With w7 your example has the weight increasing (0.5 -> ~0.51), but it appears it should be decreasing since the output is higher than expected (~0.7 -> 0.1).
I know this is an older post, but if you could double check those values and let me know, that would help me a lot.
:)
Thank you Matt for your very good explanation! How do you create the figures of the basic structre, … etc. ?
Hi I need help, please have someone help me
What is your problem?
that was very nice
could the problem be solved linear programming ?
Wonderful explanation, sir!
I’m stuck at calculating w1. The procedure says to calculate dEtotal/dw1 we need dEo1/douth1, proceeds to use the chain rule, and substitutes 0.74136507 for dEo1/douto1. 0.74136507 was earlier given as the value of dEtotal/douto1. What am I missing? Why are the values the same? How is dEo2/douto1 calculated? Thanks in advance!
I actually got it after a few repeat attempts. The key is, of course, in using the chain rule more to go deeper from d/dout to d/dnet. It’s then possible to calculate everything.
why the w1 partial derivative formula is not,
i.hizliresim.com/nQlkpa.jpg
Am I wrong?
I think neth1 will be 0,25*0,10, not 0,2*0,10, because w3=0,25. Am I wrong ?
Yes I am wrong :))
Excellent !!! realy great ! thx !!
This was one of the best tutorials which helped me have a firm understanding of the dynamics of backpropagation algorithm in NN. Thanks man. Be blessed.
Excellent!
But, is bias value need to be updated as weight?
One question: in the explanation of the chain rule (the image) why is w6 connected to h2? w6 is connected to h1 in the image, right? Only w7 and w8 are connected to h2.
i dunno how that -1 come from cost function derivative, someone help
Same here, not clear!
Derivative of 2nd degree polinomial expression x derivative of the expression in pharentesis that is minus one
Thanks!
That’s the best explanation I found since the first time I read about BP. Thanks!
One of the best explanations I have seen. Thanks a lot, Matt!
what if i do not know the weights and hidden layers, how do i proceed
Great !!!
thank you, it is really helpful to understand Backpropagation
Why n=0.5? I couldn’t understand. Please help.
Please explain, why n=0.5? Thanks in advance
Hello, Matt. Just made all stuff as it was layed here, all works fine. I additionally tried to make backpropagation for NiN (network in network type). All is work, but not well when I try to get use it for detection problem (here I need spatial data too). I suppose I make mistake in the every first layer during backprop. Could you have time to help me to desolve the problem? Maybe somebody from here can helps mee too – a.alexeev3@yahoo.com
Thank you..this is very clearly explained
Exellent post! More complex mathematical bacground of backpropagation algorithm you can find in https://learn-neural-networks.com/backpropagation-algorithm/.
This article is incredible awesome !!
Thank you so much for sharing !!
Finally got how backprop works ;-)
Thats damn lucid explanation with every step covered
very helpfull, thank a lot