Background
Backpropagation is a common method for training a neural network. There is no shortage of papers online that attempt to explain how backpropagation works, but few that include an example with actual numbers. This post is my attempt to explain how it works with a concrete example that folks can compare their own calculations to in order to ensure they understand backpropagation correctly.
Backpropagation in Python
You can play around with a Python script that I wrote that implements the backpropagation algorithm in this Github repo.
Continue learning with Emergent Mind
If you find this tutorial useful and want to continue learning about AI/ML, I encourage you to check out Emergent Mind, a new website I’m working on that uses GPT-4 to surface and explain cutting-edge AI/ML papers:

In time, I hope to use AI to explain complex AI/ML topics on Emergent Mind in a style similar to what you’ll find in the tutorial below.
Now, on with the backpropagation tutorial…
Overview
For this tutorial, we’re going to use a neural network with two inputs, two hidden neurons, two output neurons. Additionally, the hidden and output neurons will include a bias.
Here’s the basic structure:

In order to have some numbers to work with, here are the initial weights, the biases, and training inputs/outputs:
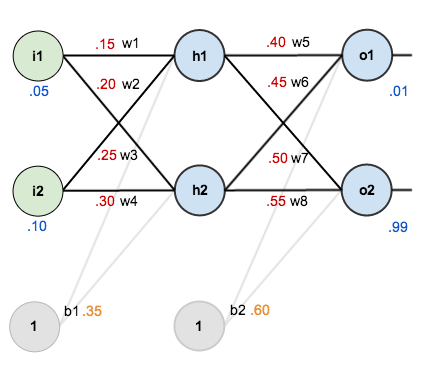
The goal of backpropagation is to optimize the weights so that the neural network can learn how to correctly map arbitrary inputs to outputs.
For the rest of this tutorial we’re going to work with a single training set: given inputs 0.05 and 0.10, we want the neural network to output 0.01 and 0.99.
The Forward Pass
To begin, lets see what the neural network currently predicts given the weights and biases above and inputs of 0.05 and 0.10. To do this we’ll feed those inputs forward though the network.
We figure out the total net input to each hidden layer neuron, squash the total net input using an activation function (here we use the logistic function), then repeat the process with the output layer neurons.
Here’s how we calculate the total net input for :
We then squash it using the logistic function to get the output of :
Carrying out the same process for we get:
We repeat this process for the output layer neurons, using the output from the hidden layer neurons as inputs.
Here’s the output for :
And carrying out the same process for we get:
Calculating the Total Error
We can now calculate the error for each output neuron using the squared error function and sum them to get the total error:
For example, the target output for is 0.01 but the neural network output 0.75136507, therefore its error is:
Repeating this process for (remembering that the target is 0.99) we get:
The total error for the neural network is the sum of these errors:
The Backwards Pass
Our goal with backpropagation is to update each of the weights in the network so that they cause the actual output to be closer the target output, thereby minimizing the error for each output neuron and the network as a whole.
Output Layer
Consider . We want to know how much a change in
affects the total error, aka
.
By applying the chain rule we know that:
Visually, here’s what we’re doing:

We need to figure out each piece in this equation.
First, how much does the total error change with respect to the output?
is sometimes expressed as
When we take the partial derivative of the total error with respect to , the quantity
becomes zero because
does not affect it which means we’re taking the derivative of a constant which is zero.
Next, how much does the output of change with respect to its total net input?
The partial derivative of the logistic function is the output multiplied by 1 minus the output:
Finally, how much does the total net input of change with respect to
?
Putting it all together:
You’ll often see this calculation combined in the form of the delta rule:
Alternatively, we have and
which can be written as
, aka
(the Greek letter delta) aka the node delta. We can use this to rewrite the calculation above:
Therefore:
Some sources extract the negative sign from so it would be written as:
To decrease the error, we then subtract this value from the current weight (optionally multiplied by some learning rate, eta, which we’ll set to 0.5):
We can repeat this process to get the new weights ,
, and
:
We perform the actual updates in the neural network after we have the new weights leading into the hidden layer neurons (ie, we use the original weights, not the updated weights, when we continue the backpropagation algorithm below).
Hidden Layer
Next, we’ll continue the backwards pass by calculating new values for ,
,
, and
.
Big picture, here’s what we need to figure out:
Visually:
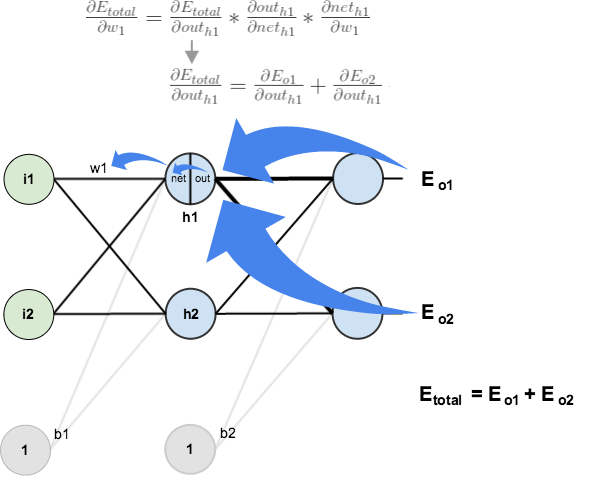
We’re going to use a similar process as we did for the output layer, but slightly different to account for the fact that the output of each hidden layer neuron contributes to the output (and therefore error) of multiple output neurons. We know that affects both
and
therefore the
needs to take into consideration its effect on the both output neurons:
Starting with :
We can calculate using values we calculated earlier:
And is equal to
:
Plugging them in:
Following the same process for , we get:
Therefore:
Now that we have , we need to figure out
and then
for each weight:
We calculate the partial derivative of the total net input to with respect to
the same as we did for the output neuron:
Putting it all together:
You might also see this written as:
We can now update :
Repeating this for ,
, and
Finally, we’ve updated all of our weights! When we fed forward the 0.05 and 0.1 inputs originally, the error on the network was 0.298371109. After this first round of backpropagation, the total error is now down to 0.291027924. It might not seem like much, but after repeating this process 10,000 times, for example, the error plummets to 0.0000351085. At this point, when we feed forward 0.05 and 0.1, the two outputs neurons generate 0.015912196 (vs 0.01 target) and 0.984065734 (vs 0.99 target).
If you’ve made it this far and found any errors in any of the above or can think of any ways to make it clearer for future readers, don’t hesitate to drop me a note. Thanks!
And while I have you…
Again, if you liked this tutorial, please check out Emergent Mind, a site I’m building with an end goal of explaining AI/ML concepts in a similar style as this post. Feedback very much welcome!

thanks!
After this line :
“`
Here’s how we calculate the total net input for h_1:
“`
instead of w2 there should be w3. means w1*i1 + w3*i2 + b1*1
yes, this part doesn’t make sense with the diagram, and I think should be corrected.
I stand corrected, w2 is the weight from i2 to h1, and w3 is the weight from i1 to h2
You forgot to include how bias is updated.
Great!
Good job !, I like the way you explain stuff…..
Thank you for your writing. It’s really interested.
Dear Sir Mazur, I cant thank you enough for your exquisite tutorial. My only question is the following.
If we had more hidden layers, lets say 2, how can I calculate the derivative θΕ(tot)/θout(h-1), in order to correct the weights linking my input neurons with the first h.l. neurons? In the second hidden layer we wouldn’t have that kind of problem since we can link θΕ(tot)/θout(h1)=θΕ1/θout(h1)+θΕ2/θout(h1) as you wrote, but for a previews layer there is not “Error association”, as far as I can perceive. I apologise if my question is not well stated.
Thank you in advance
Thank you so much. it is really interesting and very helpful.
Looks like you have an error in one of your formulas:
net_{h1} = w_{1} * i_{1} + w_{2} * i_{2} + b_{1} * 1
should be:
net_{h1} = w_{1} * i_{1} + w_{3} * i_{2} + b_{1} * 1
The diagram should have better spacing to eliminate the confusion, but,
w2 is the weight from i2 to h1, and w3 is the weight from i1 to h2
So his formula is good.
Excellent examples with simple explanations. Thank you
Awesome!
The Second formula under section: Hidden Layer
should be
\frac{\partial E_{total}}{\partial out_{h1}} = \frac{\partial E_{tot}}{\partial out_{h1}} + \frac{\partial E_{tot}}{\partial out_{h1}} rt?
instead of
\frac{\partial E_{total}}{\partial out_{h1}} = \frac{\partial E_{o1}}{\partial out_{h1}} + \frac{\partial E_{o2}}{\partial out_{h1}}
how it be used in DL,I mean calculated in image process(2 demension signal process),such as CNN.
Hi, I’m new to this topic so pardon me for asking simple questions or having wrong concepts. I understand that backpropagation algorithm uses gradient descent to find the minimized error, but you did not mention in your example that it stops when it reaches the minimum error value? Or rather, how do you know when you can stop the algorithm in this example?
Usually people set epoch. For example epoch = 10000, neural network will run 10000 times(forward and backward propagation).If they are not satisfied with the result they will tweak number of epoch.
Hi Melodytch, lets I explain with an example. You have 1020 data input and you feed your network 1000 data as training and 20 as test data set. anytime you training data, you calculate error with this formula: MAPE=( |output-target| / target ) * 100 , and calculate this for test data separately. any iteration control the MAPE for the test if MAPE for test improves, it is mean your network get a better result to predict. When MAPE for train improved but MAPE for test stop and get worse its mean your network come to overfitting and you should stop training.
We have other methods for stop training such as fix training epoch(iteration), those other friends mention about that.
Great Explanation! Thanks a ton!!!
really very helpful
One of the best explanation for back-propagation that I have come across. Thank you!
Dear Matt,
I have been studying Machine Learning and Neural Networks intensely for the past 9 months and this IS the best explanation I have come across (including 2 online MOOC’s – Stanford and Johns Hopkins Universities). Brilliant!
Bet regards,
Derrick Attfield
Thank you so much Matt ! You have explained the basic working backpropagation which is very helpful for the beginners of ML ! :)
Some of the best stuff I’ve read, extremely clear using a concrete example!
However, I would so much have appreciated that you did your calculations using Cross Entropy instead of (or in addition to!) the Squared Error as error function. Also, I’ll also point out that you do not calculate the Bias change (and the nodes should have separate biases..)
Also, while you’re at it (!), how does the derivation change using ReLU’s instead of Standard Logistc?
Great Explanation
Great class! Thank you.
very good thing .
This was very helpful for me. Thanks!
I would like to thank for this post and I would like to make one question about the partial derivative of the sigmoid function for out_o1 and out_h1.
the partial derivative of the function: out_o1=1/(1+exp(-net_o1) ) with respect to the net_o1 in this post is : out_1*(1-out_o1) why not :net_o1*(1-net_o1)?
Hi there! Really need to clarify this point.
What steps will neural network run in case of a real data set? Let’s say, we run first record and found some error rate – e1. Will we pass forward our first record’s values again after finishing backpropagation with new weights or new weights will be applied to next record?
in other words, should we keep running backpropagation for one record until its weights are unsatisfactory?
Great article indeed. I could not find any better resource than this one that explains backpropagation with an example.. Thanks for taking time to write this. This helped me a lot.
thank you this was very helpful!
Great, thanks
Thank you for your nice example.
I’m curious to know how weights of biases are updated in this example. This example includes only one starting weight for each bias.
Hi, I really like this resource. Just wanted to reiterate other comments that I read which state that each node should have a separate bias weight (b1-b4) not just one bias per layer (e.g. b1,b2). Would be good to update the images to make that clear.
https://s0.wp.com/latex.php?latex=%5Cfrac%7B%5Cpartial+net_%7Bo1%7D%7D%7B%5Cpartial+out_%7Bh1%7D%7D+%3D+w_5+%3D+0.40&bg=ffffff&fg=404040&s=0
But what if the network has two hidden layers? How am I supposed to get the weight connecting my hidden node to an output if there’s a whole other layer in between? somebody halp ;-;
Great Topic with a smooth way of explaining. is there is any article for Convolutional neural network ?
Very clear presentation and helps a lot. Thanks!
Great explanation. Good illustration and to the point.
Hi. Great article! I have a problem with computing net input for second hidden neuron in the forward pass.
Basically I put weights in a two-dimensional array, with input index and hidden neuron index. Then for every hidden neuron and for every input neuron, I calculate the net number: netNumber += weights[inputIndex][hiddenindex]*inputVectors[inputIndex];
Next, I add biases and use activation function. The result is wrong (out_h2 = 0.655318370173895), but the out_h1 gets computed correctly. Any hints?
Very comprehensive and useful example. Many thanks !
While calculating w1, shoul i use updated w5 or original w5?
original weight
No, We perform the actual updates in the neural network after we have the new weights leading into the hidden layer neurons (ie, we use the original weights, not the updated weights, when we continue the backpropagation algorithm below).
Original
The forward pass and backward pass consists of one epoch.In this one epoch the weights are being updated using the just immediate previously calculated weights.
Since in this example,the author has updated the weights only once,so the original value of w5 is to be used here.
Really good tutorial Matt. I finally had something like a “aha” moment ;-)
With the inspiration of this tutorial I translated this real number example into matrix multiplication operations.
Hello, thanks for your explanation. Can you please clarify why the biases b1 and b2 are the same for their entire
respective layers? Shouldnt we have a bias vector b of the same length as the number of neurons per layer?
Like to print things out and read over. Seems like the print out starts omitting detail once it hits the hidden layers. Odd. All in all this is quite helpful to understand the back propagation.
Really appreciate this, thanks!
thank you very much best explaining i have ever seen
that was very helpful < thanx from a fighter in
mahadi army